고정 헤더 영역
상세 컨텐츠
본문

y<x1w1+x2w2 ==1
y≥x1w1+x2w2 ==0
가중치 곱+편향의 값이 y를 초과한다면 1(True)를 출력한다.
가중치 곱+편향의 값이 y의 미만이라면 0(False)를 출력한다.
and gate or gate
1 1 1 1 1 1
0 1 0 0 1 1
1 0 0 1 0 1
0 0 0 0 0 0
nand gate xor gate
1 1 0 1 1 0
0 1 1 0 1 1
1 0 1 1 0 1
0 0 1 0 0 1

위의 그래프는 (1 1 1) 을 갖고있는 and gate의 좌표평면이다.

위의 좌표평면은 단순한 선형의 직선으로는 분류가 불가능하다.
이것이 하나의 선형 모델의 한계이다. 이 문제를 해결하기 위해서는 다층 퍼셉트론이 필요하다.
XOR 게이
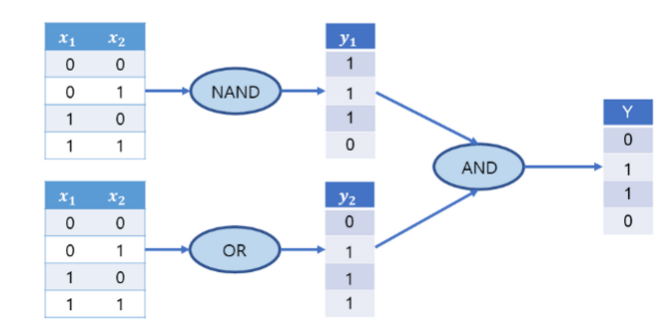
트는 NAND, OR의 출력값에 AND를 넣어주면 만들 수 있다.
XOR게이트를 사용하면 비선형 구조를 사용하여 기존의 문제를 해결 할 수 있다.
다층 퍼셉트론의 장단점
- 하나의 선으로 해결할 수 없는 문제들을 해결해준다.
- 그러나 학습시간이 오래걸린다는 단점이 있다.
- 학습에서 찾아야할 w와 b가 층을 쌓으면 쌓을 수록 많아진다. 그러므로 과적합이 되기가 쉬운 단점도 있다.
(한번 사용한 데이터는 버려지는 것이 아닌 다음 층에서 학습 재료로 사용하기 때문.)
- 가중치 초기 값(=임의로 선택되는 경사)에 민감해 지역최저점(Nan)에 빠지기가 쉬운 단점이 있다.
GATE의 파이썬 소스코드
# AND gate
import numpy as np
def AND(x1, x2):
x = np.array([x1, x2])
w = np.array([0.5, 0.5])
b = -0.7
tmp = np.sum(w*x) + b #b는 퍼셉트론에서 '쌔타'이고 편향이라고도 부른다.
if tmp <= 0:
return 0
else:
return 1
print("AND")
for xs in [(0, 0), (1, 0), (0, 1), (1, 1)]:
y = AND(xs[0], xs[1])
print(str(xs) + " -> " + str(y))
print("--------------------------")
# NAND gate
def NAND(x1, x2):
x = np.array([x1, x2])
w = np.array([-0.5, -0.5])
b = 0.7
tmp = np.sum(w*x) + b
if tmp <= 0:
return 0
else:
return 1
print("NAND")
for xs in [(0, 0), (1, 0), (0, 1), (1, 1)]:
y = AND(xs[0], xs[1])
print(str(xs) + " -> " + str(y))
print("--------------------------")
#OR gate
def OR(x1, x2):
x = np.array([x1, x2])
w = np.array([0.5, 0.5])
b = -0.2
tmp = np.sum(w*x) + b
if tmp <= 0:
return 0
else:
return 1
print("OR")
for xs in [(0, 0), (1, 0), (0, 1), (1, 1)]:
y = AND(xs[0], xs[1])
print(str(xs) + " -> " + str(y))
print("--------------------------")
#xor gate
def XOR(x1, x2):
s1 = NAND(x1, x2)
s2 = OR(x1, x2)
y = AND(s1, s2)
return y
print("XOR")
for xs in [(0, 0), (1, 0), (0, 1), (1, 1)]:
y = AND(xs[0], xs[1])
print(str(xs) + " -> " + str(y))
AND
(0, 0) -> 0 (1, 0) -> 0 (0, 1) -> 0 (1, 1) -> 1
NAND
(0, 0) -> 0 (1, 0) -> 0 (0, 1) -> 0 (1, 1) -> 1
OR
(0, 0) -> 0 (1, 0) -> 0 (0, 1) -> 0 (1, 1) -> 1
XOR
(0, 0) -> 0 (1, 0) -> 1 (0, 1) -> 1 (1, 1) -> 0
이 노트는 제가 개인적으로 공부한 내용이므로 틀린점이 있을 수 있습니다.
틀린점이 있다면 한수 가르쳐주세요ㅎㅎ
'딥러닝 기초 이론 > 밑바닥부터 시작하는 딥러닝 이론' 카테고리의 다른 글
| 7.수치미분과 기울기 (0) | 2023.01.22 |
|---|---|
| 6.엔트로피 (0) | 2023.01.22 |
| 4.손실함수 (0) | 2023.01.22 |
| 3.인공신경망 (0) | 2023.01.22 |
| 2.활성화 함수(Activation Function) (0) | 2023.01.22 |




