3.인공신경망

위의 그림에서 Zn은 시그모이드 함수를 적용시킨다는 의미이 각 층의 마지막 레이어에서는 시그모이드 함수가 아니라 소프트맥스 변환을 적용

<소프트맥스 함수>

소프트맥스 함수(Softmax Function)는 n 차원 벡터에서 특정 출력 값이 k 번째 클래스에 속할 확률을 계산합니다.

클래스에 속할 확률을 계산하는 활성화 함수이므로, 은닉층(Hidden Layer)에서 사용하지 않고 출력층(Output Layer)에서 사용됩니다.

소프트맥스 변환은 다층 신경망의 제일 마지막 층에서 출력을 변환할 때 쓰인다.

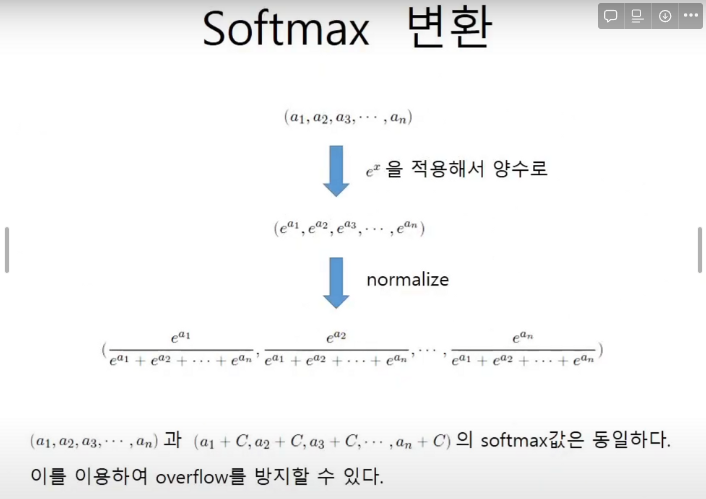
Softmax(소프트맥스)는 입력받은 값을 출력으로 0~1사이의 값으로 모두 정규화하며 출력 값들의 총합은 항상 1이 되는 특성을 가진 함수이다.

그리고 소프트맥스 변환을 한다면 결국 값은 동일해진다.

소프트맥스 함수를 구현할 때에는 오버플로우 대책이 중요하다.

오버플로우:컴퓨터 내에서 메모리에 표현하는 숫자의 값이 너무 커서 무한으로 표현되는 현상

 

def softmax(x):
c = np.max(x)
    exp_x = np.exp(x-c) # 오버플로 방지
    sum_exp_x = np.sum(exp_x)
    y = exp_x / sum_exp_x

    return y

 

위의 코드는 소프트맥스의 오버플로를 방지하는 파이썬 함수식이다.

exp_x = np.exp(x-c) 코드에서 x에서 c를 빼도 수학적으로 소프트맥스 함수의 값은 변하지 않는다.

 

#인공신경망 행렬곱
import numpy as np

def sigmoid(x):
return 1/(1+np.exp(-x))
    
def identity_function(x):
return x

def init_network():
network = {}//딕셔너리 타입
    network['W1'] = np.array([0.1,0.3,0.5],[0.2,0.4,0.6])
    network['b1'] = np.array([0.1,0.2,0.3])
    network['W2'] = np.array([0.1,0.4][0.2,0.5],[0.3,0.6])
    network['b2'] = np.array([0.1,0.2])
    network['W3'] = np.array([0.1,0.3],[0.2,0.4])
    network['b3'] = np.array([0.1,0.2])
    
    return network
    
def forward(network, x):
W1, W2, W3 = network['W1'], network['W2'], network['W3']
    b1, b2, b3 = network['b1'], network['b2'], network['b3']
    
    a1 = np.dot(x, W1) + b1
    z1 = sigmoid(a1)
    a2 = np.dot(z1, W2) + b2
    z2 = sigmoid(a2)
    a3 = np.dot(z2, W3) + b3
    y = identity_function(a3)#항등함수(있으나 없으나 똑같지만 일관성을 위해서 쓴것이다. 
                             #층수가 높아진다면 소프트맥스 함수를 적용한다.)
    
    return y
    
network = init_network() #신경망 설정
x = np.array([1.0,0.5]) #자극치 설정
y = forward(network, x) #순전파 실시

print(y) #[0.31682708 0.69627909]